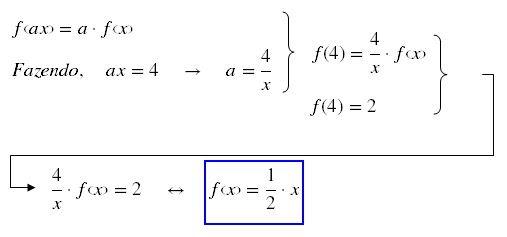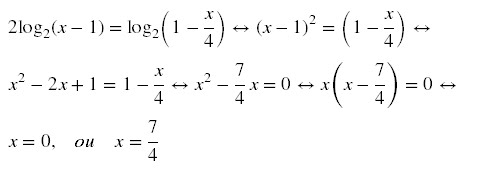EX-01 (FUVEST 2000)
a) Esboce, para
x real, o gráfico da função f(x) = |x-2| + |2x +1| ‒
x ‒ 6. O símbolo |a| indica o valor absoluto
de um número real a e é definido por |a| = a, se a ≥
0 e |a| = ‒ a, se a < 0.
b) Para que
valores reais de x, f(x) > 2x + 2.
Solução:
a)
b)
EX-02 (FUVEST 2004)
Seja m ≥
0 um número real e sejam f e g funções reais definidas por f(x) = x² ‒
2|x| + 1 e g(x) = mx + 2m.
a) Esboçar no
plano cartesiano representado ao lado, os gráficos de f e g quando m = 1/4 e m
= 1.
b) Determinar as
raízes de f(x) = g(x) quando m = 1/2.
c) Determinar,
em função de m, o número de raízes da equação f(x) = g(x).
Solução:
a)
f(x) = x² ‒
2|x| + 1 e g(x) = mx + 2m.
x ≥ 0, f (x) = x² ‒ 2x +
1 = (x ‒ 1)²
x < 0, f (x) = x² + 2x + 1 = (x + 1)²
m = 1/4, g(x) = 1/4x + 2/4 = 1/4x + 1/2
m = 1, g(x) = x + 2
Portanto, o gráfico fica:
b)
f(x) = g(x), m =
1/2.
f(x) = x² ‒ 2|x| + 1
g(x) = mx + 2m. = x/2 + 1
c)
As raízes de
f(x) = g(x) são as abscissas dos pontos onde os gráficos de f e g se
interceptam.
Sendo f(x) = x² ‒
2|x| + 1 e g(x) = mx + 2m.
Variando m,
temos:
Resposta:
Para m = 0, a equação possui duas
raízes reais (‒1, 1).
Para m = 1/2, a
equação possui três raízes reais.
Para 0 < m
< 1/2 , a equação possui quatro raízes reais.
Para m > 1/2,
a equação possui duas raízes reais.
EX-03 (FUVEST 2005)
Seja f(x) = ax²
+ (1-a)x + 1, onde a é um número real diferente de zero.
Determine os
valores de a para os quais as raízes da equação f(x0 = 0 são reais e o número x
= 3 pertence ao intervalo fechado compreendido entre as raízes.
Solução:
Como x = 3
pertence ao intervalo entre as raízes, temos as seguintes possibilidades:
Observamos que o
produto a.f(x) é negativo em ambas as possibilidades; então podemos escrever
que:
As
raízes são a = 0 e a = ‒ 2/3; como f(x) é uma função do segundo
grau, devemos ter que “a” é diferente de zero.
Portanto, a
resposta é: [‒
2/3, 0 [
Outra maneira de
analisar os valores de “a” para que a.f(x) ≤ 0.
A resposta
é: [‒ 2/3, 0 [
EX-04 (FUVEST 2006)
Uma função f
satisfaz a identidade f(ax) = af(x) para todos os números reais a e x. Além
disso, sabe-se que f(4) = 2. Considere ainda a função g(x) = f(x-1)+1 para todo
o número real x.
a) Calcule g(3)
b) Determine
f(x), para todo x real.
c) Resolva a
equação g(x) = 8.
Solução:
Dados –
1)
f(ax)
= af(x), quaisquer a, x pertencentes a reais
2)
f(4)
= 2
3)
g(x)
= f(x-1)+1, qualquer x pertencente a reais
a)
b)
c)
EX-05 (FUVEST 2007)
a) Represente,
no sistema de coordenadas desenhado na folha de respostas ao lado, os gráficos
das funções f(x) = |4 ‒ x²| e g(x) = (x + 7)/2
b) Resolva a
inequação |4 ‒ x²| ≤ (x + 7)/2
Solução:
a)
|4 ‒
x²| = |‒ x² + 4|
Se ‒
x² + 4 = 0, então as raízes são
‒ 2 e 2. Portanto, temos:
b)
Para x ≤ 2 ou x ≥ 2, tem-se
‒ 4 + x² = (x + 7)/2 ↔ ‒ 8 + 2x² = x +
7 ↔ 2x² - x – 15 =
0 ↔ (x + 5/2)(x ‒ 3) = 0 ↔
↔ x = ‒ 5/2
ou x = 3
Parra ‒
2 ≤ x ≤ 2, tem-se:
4 ‒
x² = (x + 7)/2 ↔ 8 ‒ 2x² = x + 7 ↔ ‒ 2x² ‒
x + 1 = 0 ↔ (x + 1)(x ‒1/2) = 0 ↔
↔ x = ‒ 1 ou
x = 1/2
Colocando as
abscissas no gráfico, tem-se:
Portanto, f(x) ≤
g(x) se, somente se,
EX-06 (FUVEST 2009)
Para cada número
real m, considere a função quadrática f(x) = x² + mx + 2.
Nestas
condições:
a) Determine em
função de m, as coordenadas do vértice da parábola de equação y = f(x).
b) Determine os
valores de m ϵ R para os quais a imagem de f contém o
conjunto {y ϵ R: y ≥ 1}.
c) Determine o
valor de m para o qual a imagem de f é igual ao conjunto {y ϵ R:
y ≥ 1} e, além disso, f é crescente no
conjunto {y ϵ R: x ≥ 0}.
d) Encontre,
para a função determinada pelo valor de m do item c) e para cada y ≥
2, o único valor de x ≥ 0 tal que f(x) = y.
Solução:
a) Sabemos que
as coordenadas do vértice (xv,yv) de uma parábola é dada
pelo par (‒ b/2a, ‒ ∆/4a), onde a e b
são coeficientes da função ax² + bx +c; e ∆ (delta) = b² ‒
4ac.
Portanto, temos:
a = 1
b = m
c = 2
b)
Como a > 0 (a
= 1) a concavidade está virada para cima, então o conjunto imagem Im é:
Para ter {y ϵ
R / y ≥ 1} contido no conjunto Im, basta impor yv
≤ 1, então:
c)
Para Im = {y ϵ
R / y ≥ 1} e f crescente no {x ϵ
R / x ≥ 0} devemos ter:
d)
Para m = 2,
temos f(x) = x² + 2x +2.
Logo, se x ≥
0 e y ≥ 2, temos:
Como para cada y
≥ 2 existe apenas um único x ≥ 0, como podemos ver
no gráfico, então:
EX-07 (FUVEST 2010)
Determine a
solução (x, y), y > 1, para o sistema de equações:
Solução:
(II) em (I)
Como y > 1, então, o par (x,y) procurado é: (11, 2)
EX-08 (FUVEST 2011)
Determine o
conjunto de todos os números reais x para os quais vale a desigualdade:
Solução:
Primeiramente,
as condições de existência:
Fazendo a
intersecção de (1) e (2), temos:
EX-09 (FUVEST 2012)
Determine para
quais valores reais de x é verdadeira a desigualdade |x² ‒
10x + 21| ≤ |3x – 15|.
Solução:
A idéia é
esboçar o gráfico para responder a questão.
Determinando as
intersecções entre as curvas |x² ‒ 10x + 21| e |3x ‒
15|:
Então, temos:
x² ‒
10x + 21 = 3x ‒ 15
ou x² ‒
10x + 21 = ‒ 3x + 15 →
→
x² + 3x + 36 = 0 ou x² ‒ 7x + 6 = 0 → (x ‒ 4)(x ‒
9) = 0 ou (x ‒ 1)(x ‒
6) = 0 →
→ x
= 4 ou
x = 9 ou x = 1
ou x = 6
Esboçando o
gráfico das funções:
Do gráfico
podemos concluir que desigualdade |x² ‒ 10x + 21| ≤
|3x – 15| é verdadeira para:
1 ≤ x ≤ 4
ou 6 ≤ x ≤ 9
EX-10 (FUVEST 2014)
Dados m e n
inteiros, considere a função f definida por:
para x ≠
‒ n.
(a) No caso em
que m = n = 2, mostre que a igualdade f(√2) = √2
se verifica.
(b) No caso em
que m = n = 2, ache as intersecções do gráfico de f com os eixos coordenados.
(c) No caso em
que m = n = 2, esboce a parte do gráfico
de f em que x > ‒ 2, levando em conta as informações
obtidas nos itens (a) e (b). Utilize o par de eixos dado na página de
respostas.
(d) Existe um
par de inteiros (m, n) ≠ (2, 2) tal que a condição f(√2)
= √2 continue sendo satisfeita?
Solução:
(a) m = n = 2
(b)
Como f(x) = 0 ↔
2 – 2/(x + 2) = 0 ↔ x = –1 e f(0) = 2 – 2/(0 +2) =1, os pontos de
intersecção de f com os eixos coordenados são (–1; 0) e (0; 1). Veja a figura.
(c)
O gráfico de f para m
= n = 2 e x > –2, fica como:
d)
Como (m + 2 – 2n ) ϵ
Z e (2 – n) ϵ Z, a igualdade será satisfeita se, e somente
se,
(m + 2 – 2n) = 0
e (2 – n) =0
Portanto, n = 2
e m = 2 → m = n = 2
Logo, não existe (m, n) ≠ (2, 2) tal que f(√2)
= √2. (o que se pode verificar no gráfico do item anterior).
EX-11 (FUVEST 2015)
Resolva as
inequações:
a) x³ ‒
x² ‒ 6x > 0;
b) log2
(x³ ‒ x² ‒ 6x) ≤
0
Solução:
a)
Vamos procurar
as raízes da equação x³ ‒ x² ‒ 6x = 0.
Assim, o gráfico
é:
Pelo gráfico,
temos:
x³ ‒ x² ‒ 6x > 0 ↔ ‒ 2
≤ x ≤ 0 ou x > 3
Assim, o conjunto
solução da inequação é:
b)
log2
(x³ ‒ x² ‒ 6x) ≤
2
x³ ‒
x² ‒ 6x ≤ 2² ↔ x³ ‒ x² ‒
6x ≤ 4
↔
x³ ‒ x² ‒ 6x ‒
4 ≤ 0 (1)
Vamos considerar
a equação x³ ‒ x² ‒ 6x ‒
4 = 0, cuja raiz igual a ‒
1; pois
(‒
1)³ ‒ (‒ 1)² ‒
6.(‒ 1) ‒ 4 = 0.
Aplicando o
dispositivo de Briot-Ruffini, temos que:
Logo,
x³ ‒
x² ‒ 6x ‒ 4 =
0 ↔ (x + 1)(x² ‒ 2x ‒ 4) = 0 ↔
(x + 1) = 0 ou (x² ‒ 2x ‒ 4) = 0
Portanto,
x = ‒
1 ou x = 1 + √5 ou x = ‒ √5
Colocando no
gráfico, temos:
Solução da
inequação x³ ‒ x² ‒ 6x ‒ 4 ≤
0 é: x ≤ 1 ‒ √5,
ou ‒ 1 ≤ x ≤ 1 + √5
Verificando a
condição de existência: x³ ‒ x² ‒ 6x > 0 (= item a
da questão)
x³ ‒ x² ‒ 6x > 0 ↔ ‒ 2
≤ x ≤ 0 ou x > 3
Logo, o conjunto
solução da inequação é:
Respostas:
EX-12 (FUVEST 2015)
A função f está
definida da seguinte maneira: para cada inteiro ímpar n,
(a) Esboce o
gráfico f para 0 ≤ x ≤ 6.
(b) Encontre os
valores de x, 0 ≤ x ≤ 6, tais que f(x) =
1/5.
Solução:
(a)
0 ≤
x ≤ 6 → n = 1, 3, 5
A) Para 0 ≤
x ≤ 2, temos n = 1 e f é definida por:
B) Para 2 ≤
x ≤ 4, temos n = 3 e f é definida por:
C) Para 4 ≤
x ≤ 6, temos n = 5 e f é definida por:
Assim, o gráfico de f para 0 ≤ x ≤ 6 é:
b)
Se 0 ≤ x ≤ 6 e
f(x) = 1/5; do item a, temos:
Pelo gráfico
temos:
Portanto, temos:
EX-13 (FUVEST 2016)
Considere as
funções f e g definidas por:
a) Calcule
f(3/2), f(2), f(3), g(-4), g(0) e g(2).
b) Encontre x,
1< x < 4, tal que f(x) = g(x).
c) Levando em
conta os resultados dos itens a) e b), esboce os gráficos de f e g no sistema
cartesiano impresso na página de resposta.
Solução:
a)
b)
x, 1 < x <
4 tal que f(x) = g(x).
Como x = 0 não
convém, portanto a resposta é x = 7/4, pois 1 < x < 4.
c)
EX-14 (FUVEST 2016)
A figura abaixo
representa o gráfico de uma função f:[‒5,5]. Note que f(‒5)=f(2)
= 0. A
restrição de f ao intervalo [‒5, 0] tem como gráfico parte de uma
parábola com vértice no ponto (‒2, ‒3); restrita ao
intervalo [0,5], f tem como gráfico um segmento de reta.
Os sistemas de eixos
da folha de respostas
a) Calcule f(‒1)
e f(3);
Usando os
sistemas de eixos da folha de respostas, esboce:
b) o gráfico de
g(x) = |f(x)|, x ϵ [‒5,5];
c) o gráfico de
h(x) = f(|x|), x ϵ [‒5,5].
Solução:
Para a parábola:
Se uma das
raízes é ‒ 5 e a abscissa do vértice é ‒
2, por simetria, a outra raiz é 1, assim:
f(x) =
a.(x+5).(x‒1), para x ϵ [‒
5, 0]
Vértice: (‒2,
‒3), portanto; para calcular o valor de a, temos:
f(‒2)
= ‒3 ↔ a.(‒2+5).(‒2‒1)
= ‒3 ↔ a.(3).(‒3)
= ‒3 ↔ a = 1/3
Logo: f(x) = 1/3.(x+5).(x‒1), para x ϵ [‒5,
0]
Para reta:
Para o intervalo
[0, 5] a reta é do tipo f(x) = mx + n.
Da equação da
reta:
f(2) = 0 ↔
0 = m.2 + n ↔ 2m + n = 0
Da equação da
parábola:
f(0) = 1/3.(0 +
5).(0 ‒ 1) = ‒ 5/3 ↔
f(0) = ‒ 5/3
Da equação da
reta:
f(0) = m.0 + n,
então, ‒ 5/3 = n ↔ n = ‒
5/3
0 = 2m + n
˃ 0
= 2m ‒ 5/3
↔ 2m = 5/3
↔ m = 5/6
n = ‒
5/3
Logo a equação
da reta é: f(x) = 5/6x ‒ 5/3 para x ϵ [0, 5]
Resumindo:
a)
f(‒1) =
1/3.(‒1+5).(‒1‒1) = ‒ 8/3 ↔ f(‒1)
= ‒ 8/3
f(3) = 5/6.3 ‒
5/3 = 5/6 ↔ f(3) = 5/6
b)
Se f(x) ≥ 0,
então g(x) = |f(x)| = f(x), assim o gráfico de f e g são iguais.
Se f(x) ≤
0, então g(x) = |f(x)| = ‒ f(x), assim o gráfico de g é o gráfico e
f rebatido entorno do eixo das abscissas.
Portanto, o
gráfico fica:
c)
Se x ≥
0, então h(x) = f(|x|) = f(x), assim h e
f têm o mesmo gráfico.
Se x ≤
0, então h(x) = f(|x|) = f(‒x) = ‒ 5/6x ‒
5/3, assim o gráfico de h(x) é a função f(x) rebatido entorno do eixo das
ordenadas, para intervalo [0,5].
Portanto o
gráfico fica: