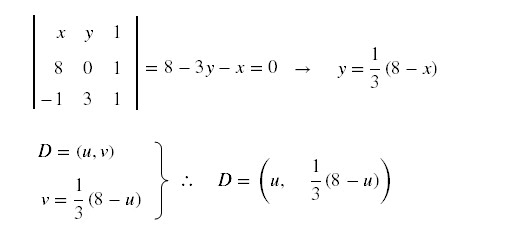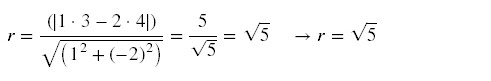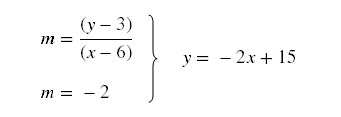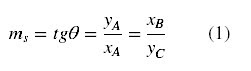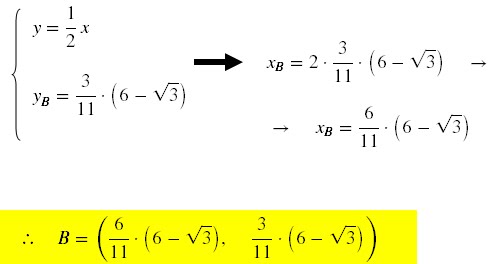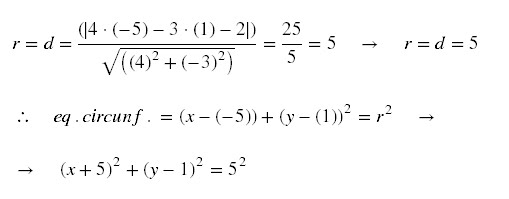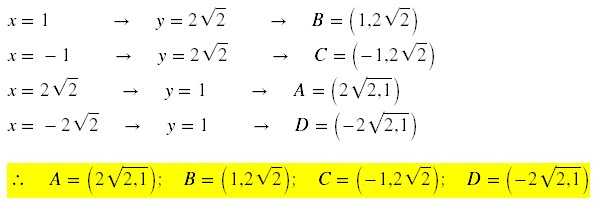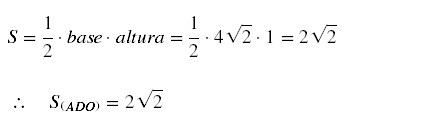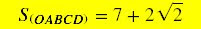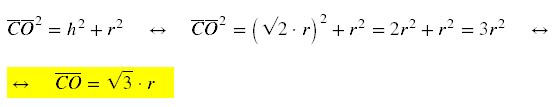Ex-01 (FUVEST 2001)
A hipotenusa de um
triângulo retângulo está contida na reta r : y = 5x – 13 e um de seus catetos
está contido na reta s: y = x – 1. Se o
vértice onde está o ângulo reto é um ponto da forma (k,5) sobre a reta s, determine:
a) todos os vértices do
triângulo;
b) a área do triângulo.
Solução:
Desenhando no plano
cartesiano os dados do enunciado, tem-se:
Como o vértice A (k,5)
pertence à reta s, então, podemos escrever que:
O vértice C é a
intersecção das retas r e s, então:
Para determinar as
coordenadas do vértice B(x,y), vamos aplicar o conceito de distância de dois
pontos e Teorema de Pitágoras, por se tratar de um triângulo retângulo.
Distância entre 2 pontos:
Teorema de Pitágoras:
Os vértices são: A(6,5), B(4,7), C(3,2)
b) Área do triângulo ABC:
Sabemos que a área é igual
à metade, em módulo, do determinante dos vértices.
Outra opção para resolver o item (a):
Para determinação dos
vértices A e C – é o mesmo.
Porém, para calcular o
vértice B vamos aplicar o conceito de perpendicularidade de duas retas.
Seja m o coeficiente
angular da reta, então, tem-se:
Ex-02 (FUVEST 2002)
Sejam A=(0,0), B=(8,0) e
C=(-1,3) os vértices de um triângulo e D=(u,v) um ponto do segmento BC. Sejam E o ponto de intersecção de AB com a
reta que passa por D e é paralela ao eixo dos y e F o ponto de intersecção de
AC com a reta que passa por D e é paralela ao eixo dos x.
a) Determine, em função de
u, a área do quadrilátero AEDF.
b) Determine o valor de u
para o qual a área do quadrilátero AEDF é máxima.
Solução:
Determinar a equação da
reta r, para expressar as coordenadas do ponto D em termos de u:
Determinar a equação da
reta s, para expressar as coordenadas do ponto F em termos de u:
O quadrilátero AEDF é um
trapézio, portanto, a área é expressa por:
onde h = altura, B = base
maior e b = base menor
Calculando h, B e b:
Calculando o valor de u,
para que a área do trapézio AEDF seja máxima:
A área é máxima, para
abscissa do vértice. Igualando a zero a primeira derivada da expressão da área
(=equação do segundo grau) tem-se este valor.
Respostas:
Ex-03 (FUVEST 2003)
a) A reta r passa pela
origem do plano cartesiano e tem coeficiente angular m>0. A circunferência C passa
pelos pontos (1,0) e (3,0) e tem centro no eixo x. Para qual valor de m a reta
r é tangente a C?
b) Suponha agora que o
valor de m seja menor que aquele determinado no item anterior. Calcule a área do triângulo determinado pelo
centro de C e pelos pontos de intersecção de r com C.
Solução:
a)
Logo:
Equação da circunferência
C = (2,0) e raio = 1:
Equação da reta r:
Seja (x, y) um ponto
genérico da reta r e passa pela origem A = (0,0).
Então,
a equação da reta r é:
Outra opção para fazer o item (a):
Os pontos (1,0) e (3,0) pertencem
ao eixo x; e, pelo enunciado, estes pontos pertencem à circunferência e,
também, o centro pertence ao eixo x, então C = (a,0).
C = (2,0); pois a =
(1+3)/2 = 2
E como a reta passa pela
origem temos: y = mx
Logo: ‒ mx + y = 0
A reta r é tangente no
ponto T, portanto, o ângulo OTC é reto, logo podemos calcular o coeficiente
angular m, aplicando o conceito de distância de ponto à reta. Da seguinte
forma:
d =
distância do ponto C à reta r (y = mx ↔ ‒ mx + y = 0) = raio da circunferência = 1
Genericamente
C = (x0,y0), então, temos que:
Como m > 0, então,
b) Como pelo enunciado
a reta r é secante à circunferência.
h = distância do centro C
= (2,0) à reta mx – y = 0
Aplicando Pitágoras no ΔAMC
, temos:
Logo a área é igual à:
Ex-04 (FUVEST 2004)
Na figura ao lado, os
pontos A,B e C são vértices de um triângulo retângulo, sendo B o ângulo
reto. Sabendo-se que A = (0,0), B
pertence à reta x – 2y = 0 e P = (3,4) é o centro da
circunferência inscrita no triângulo ABC, determinar as coordenadas:
a) do vértice B.
b) do vértice C.
Solução:
a)
Calculando o valor do
raio, aplicando o conceito de distância (mínima) de um ponto à reta; sendo P = (3,4) e reta AB: x – 2y = 0
Determinando as
coordenadas do ponto T1:
O ponto T1 é a
intersecção da circunferência com a reta AB.
A hipotenusa AT1,
pode ser calculada utilizando Pitágoras:
E como T1B = √5, então, o lado AB (hipotenusa) é igual a:
Determinando as
coordenadas do vértice B.
Os triângulos ΔADT1 e ΔAEB
são semelhantes, então, temos que:
b)
O vértice C é a
intersecção das retas AC e BC.
Determinando a equação da
reta AC:
O m(AC) = 1/2 não pode
ser, pois, é o coeficiente angular da reta AB; portanto, a equação da reta AC
é:
Determinando a equação da
reta BC:
A reta BC passa pelo ponto
B = (6,3) e tem coeficiente angular mBC = -2 (pois, mAB*mBC
= ‒ 1 e mAB = 1/2).
Seja coordenada do vértice
C = (x,y), então temos:
O vértice C é a
intersecção das retas AC e BC, então:
Ex-05 (FUVEST 2005)
A figura representa duas
circunferências de raios R e r com centros nos pontos A e B, respectivamente,
tangenciando-se no ponto D. Suponha que:
a) As retas t1
e t2 são tangentes a ambas as circunferências e interceptam-se no
ponto C.
b) A reta t2 é
tangente às circunferências no ponto D.
Calcule a área do
triângulo ABC, em função dos raios R e r.
Solução:
Sabemos que todas as retas
tangentes a uma circunferência, são também, perpendiculares ao raio no ponto de
tangência.
Sejam E e F os pontos de
tangência da reta t1 às circunferências:
Então temos que a reta AC
é a bissetriz do ângulo FAD e a reta BC é a bissetriz do ângulo ECD.
Logo, temos que: 2α +
2β = 180º, então, α + β =
90º, portanto, o ΔABC é retângulo em C.
Sabemos que
a altura de um triângulo retângulo é igual à média geométrica entre as medidas
dos segmentos que determina sobre a base (=hipotenusa do ΔABC).
Portanto,
E como
Então,
Ex-06 (FUVEST 2005)
Na figura abaixo A, B e D
são colineares e o valor da abscissa m do ponto C é positivo. Sabendo-se que a
área do triângulo retângulo ABC é 5/2, determine o valor de m.
Solução:
Os triângulos AOD e ABC
são semelhantes.
No triângulo AOD:
Aplicando o teorema de
Pitágoras, temos que:
Como os triângulos ABC e
AOD são semelhantes, então, temos a seguinte relação de proporcionalidade:
Ex-07 (FUVEST 2006)
A reta s passa pela origem
O e pelo ponto A do primeiro quadrante. A reta r é perpendicular à reta s, no
ponto A, e intercepta o eixo x no ponto B e o eixo y no ponto C. Determine o
coeficiente angular de s se a área do triângulo OBC for o triplo da área do
triângulo OAB.
Solução:
Do enunciado, temos a
seguinte figura:
É dada a seguinte
informação:
Então,
Assim:
Portanto,
Resposta:
Outra maneira de resolver
o problema:
Da figura, temos:
Do enunciado, temos:
Portanto,
De (1) e (2), temos:
Resposta:
Ex-08 (FUVEST 2006)
a) Determine os pontos A e
B do plano cartesiano nos quais os gráficos de y = 12/x – 1 e x + y – 6 = 0 se
interceptam.
b) sendo O a origem,
determine o ponto C no quarto quadrante que satisfaz AÔB = ACB e que pertence à
reta x = 2.
Solução:
a)
Assim, os gráficos se interceptam nos pontos A (3,3) e B
(4,2).
b)
A reta AO possui
coeficiente angular mAO = 3/3 = 1 e a reta AB possui o coeficiente
angular de mAB = ‒ (3 ‒ 2)/(4 ‒ 3) = ‒
1, então o triângulo AOB é retângulo em A. Portanto, o ponto P (2,1) é o centro da
circunferência que passa pelos ponto A, B e O e o segmento BO é o diâmetro da
circunferência.
Calculando o raio da
circunferência; por Pitágoras temos:
OP² = 1² + 2² →
OP = √5
Sabendo-se que os ângulos
AOB e ACB são iguais e que o ponto C pertence à reta x=2, então podemos
concluir que este ponto pertence à circunferência que passa pelos pontos O, A e
B e que o ponto C é o ponto de menor ordenada dessa circunferência.
Nota: todos e quaisquer
pontos que pertencem ao arco AOB enxergam o segmento AB sob o mesmo ângulo;
pois o arco AOC é o arco capaz. Um arco capaz é o lugar geométrico dos pontos
que enxergam um segmento AB num determinado ângulo.
Agora, vamos determinar as
coordenadas do ponto C:
O segmento CP = √5, portanto a ordenada do ponto
C é igual a ‒ (√5 ‒ 1) = 1 ‒ √5, logo, C =
(2, 1 ‒ √5)
Resposta:
a)
A (3,3) e B (4,2)
b)
C = (2, 1 ‒ √5)
Ex-09 (FUVEST 2007)
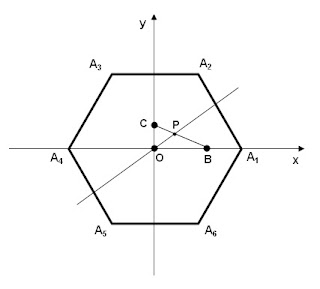
Na figura ao lado, os
pontos A1, A2, A3, A4, A5,
A6 são vértices de um hexágono regular de lado 3 com centro na
origem O de um sistema de coordenadas no plano. Os vértices A1 e A4
pertencem ao eixo x. São dados também os
pontos B = (2,0) e C = (0,1).
Considere a reta que passa
pela origem O e intersecta o segmento BC no ponto P, de modo que os triângulos
OPB e OPC tenham a mesma área. Nessas condições, determine
a) a equação da reta OP.
b) os pontos de interseção
da reta OP com o hexágono.
Solução:
a)
Do enunciado, temos:
Portanto, a equação da
reta OP é:
b)
Seja B = (xB, yB)
e como B pertence à reta OP, então temos:
B = (2yB,yB)
O coeficiente angular da
reta A1A2 é igual a m = tg 120º = ‒ √3,
então temos:
O ponto B pertence à reta
OP, portanto:
O ponto B e C são
simétricos em relação à origem (ponto O),
Ex-10 (FUVEST 2008)
São dados, no plano
cartesiano de origem O, a circunferência de equação x² + y² = 5, o ponto P =
(1, √3) e a reta s que passa por P e é paralela ao eixo
y. Seja E o ponto de ordenada positiva
em que a reta s intercepta a circunferência. Assim determine
a) a reta tangente à
circunferência no ponto E.
b) o ponto de encontro das
alturas do triângulo OPE.
Solução:
Montando a figura conforme
o enunciado, temos:
a) Vamos inicialmente
determinar as coordenadas do ponto E:
O ponto E é a intersecção
da circunferência com a reta s, então,
A equação da reta r (reta
OE) é:
A reta t tangente a
circunferência em E é perpendicular a reta r, portanto, temos:
Seja a equação da reta t:
y=mt.x+a, então, temos:
E a distância do ponto P =
(0,0) até esta reta é d = √5 (=raio), então temos:
Portanto a equação da reta
t é:
b)
Encontro das retas que
contém as alturas do triângulo EOP:
O ponto H é o ponto de
encontro das três retas que contém as alturas do triângulo EOP.
O coeficiente angular da
reta OP (reta z) é:
O coeficiente angular da
reta u (perpendicular) que contém a altura do triângulo EOP e que passa pelo
ponto E é:
Portanto, a equação da
reta u que contém a altura do triângulo EOP e que passa por E = (1,2) é:
O ortocentro (ponto H) do
triângulo EOP é ponto de intersecção da reta w de equação y=0 (altura do
triângulo EOP que passa pelo ponto O) e da reta u de equação x+√3y‒2√3‒1=0
(altura do triângulo EOP que passa pelo ponto E). Nota: obrigatoriamente, a altura do triângulo
EOP que passa pelo ponto P, a reta v, passa em H.
Resposta:
a)
x + 2y ‒ 5
= 0
b)
(2√3
+ 1; 0)
Ex-11 (FUVEST 2009)
No plano cartesiano Oxy, a
circunferência C tem o centro no ponto A = (‒5, 1) e é tangente à reta t de
equação 4x ‒ 3y ‒ 2 = 0 em um ponto P. Seja ainda Q o ponto de
intersecção da reta t com o eixo Ox. Assim:
a) Determine as
coordenadas do ponto P;
b) Escreva uma equação
para a circunferência C;
c)
Calcule a área do triângulo APQ.
Solução:
Fazendo o desenho de
acordo com o enunciado, temos:
a)
Determinando a equação da
circunferência, para determinar o ponto de intersecção P (=ponto tangente) com
a reta t.
Raio da circunferência =
distância do ponto A a reta t; então temos:
Determinando as
coordenadas do ponto P (=ponto comum entre a reta t e a circunferência):
b)
Uma equação da
circunferência:
c)
São conhecidas as
coordenadas de todos os vértices do triângulo:
As coordenadas do ponto Q:
y = 0 → 4x - 3*0 – 2 =0 → x = 1/2
A = (-5,1); P = (-1,-2); Q
= (1/2,0)
Ex-12 (FUVEST 2010)
No sistema ortogonal de coordenadas cartesianas
Oxy da figura, estão representados a circunferência de centro na origem e raio
3, bem como o gráfico da função
Nessas condições,
determine
a) as coordenadas dos
pontos A, B, C, D de intersecção da circunferência com o gráfico da função.
b) a área do pentágono
OABCD.
Solução:
a)
De (2), temos:
Em (1), temos:
b)
A área do pentágono OABCD
é igual à área do trapézio ABCD somado à área do triângulo ADO.
A área do trapézio ABCD:
A área do triângulo ADO:
A área do pentágono OABCD
é:
Ex-13 (FUVEST 2014)
Considere a circunferência
λ de equação cartesiana x²+y²-4y=0 e a parábola α de equação y=4‒x².
a) Determine os pontos
pertencentes à intersecção de λ com α.
b) Desenhe, no par de
eixos dado na página de respostas, a circunferência λ e
a parábola α. Indique,
no seu desenho, o conjunto dos pontos (x,y) que satisfazem, simultaneamente, as
inequações: x²+y²-4y ≤ 0 e y ≥ 4-x².
Solução:
a)
b)
O conjunto de pontos (x,y)
que satisfazem, simultaneamente, as inequações x²+y²-4y≤0
e y≥4-x² corresponde às áreas preenchidas de azul
escuro.
Ex-14 (FUVEST 2015)
Na figura, na página de
respostas, a circunferência de centro em O e raio r tangencia o lado BC do
triângulo ABC no ponto D e tangencia a reta AB no ponto E. Os pontos A, D e O
são colineares, AD=2r e o ângulo ACO é reto. Determine, em função de r
a) a medida do lado AB do
triângulo ABC;
b) a medida do segmento
CO.
Solução:
a)
Os triângulos retângulos
ABD e AEO são semelhantes que possuem o ângulo A em comum.
Portanto vale a relação
seguinte (de semelhança de triângulos):
Aplicando Pitágoras no ΔAEO,
temos:
Portanto, temos:
b)
De acordo com o enunciado
o triângulo ACO é retângulo em C.
Sabemos que para um
triângulo retângulo vale a relação:
Aplicando Pitágoras no
triângulo retângulo CDO, temos o valor do segmento CO:
Ex-15 (FUVEST 2016)
No plano cartesiano Oxy, a
circunferência C tem centro no ponto P=(2,1) e a reta t é tangente a C no ponto
Q = (-1,5).
a) Determine o raio da
circunferência C.
b) Encontre uma equação
para a reta t.
c)
Calcule a área do triângulo PQR, sendo R o ponto de intersecção de t com o eixo
Ox.
Solução:
Colocando no gráfico os dados do enunciado, temos;
a) O segmento PQ é igual
ao raio da circunferência.
Aplicando Pitágoras no
triângulo MPQ, temos;
b)
As retas t e PQ são
perpendiculares entre si, então:
Seja a equação da reta t:
y = mt*x + α, então:
c)
O
ponto R é intersecção de t com o eixo Ox, portanto,
Logo,
a área do triângulo PQR é:
