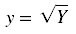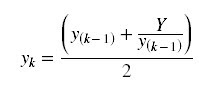Cálculo numérico da raiz quadrada - Método de Herão

Processo para calcular numericamente uma raiz quadrada de um número qualquer. As calculadoras, computadores e microprocessadores aplicam este método para extração de raiz quadrada numérica, porque converge muito rápido para o resultado.

Herão foi um matemático de destaque de Alexandria na antiguidade.

Este método é para quando se tem apenas calculadora com 4 operações aritméticas.

Calcular a seguinte raiz:

Seja y₀ a primeira aproximação da raiz quadrada de Y, então temos para a próxima aproximação melhor:

Para melhorar a aproximação devemos fazer a nova iteração:

E, assim, para n-ésima iteração, tem-se:

Quanto mais iterações, tem-se mais precisão na aproximação.

ALGORITMO

Após a escolha da aproximação inicial y₀, podemos construir o seguinte algoritmo:

Onde, para cada iteração k, para todo k = 1, 2, 3,..., encontramos uma raiz y_k mais próxima à raiz de Y.

A escolha da aproximação inicial:

Escolher o valor correspondente ao quadrado perfeito mais próximo, para que se tenha uma convergência mais rápida.

Exemplo:

Calcular a raiz de 499.