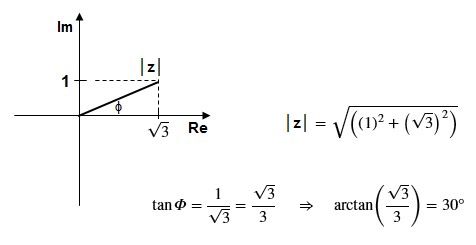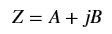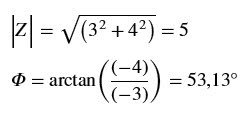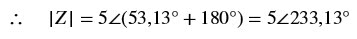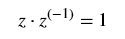Assim sendo, podemos
representar um genericamente número complexa na seguinte forma:
Onde Z é um número complexo
qualquer, A é sua parte real e B a sua parte imaginária, sendo
Os números complexos
representam o conjunto de números mais abrangente. Os números reais são um
subconjunto (Fig-01); sendo que o número real é um número complexo com a parte
imaginária igual a zero.
Os números complexos têm
muita importância em análise de circuitos elétricos. Permitem analisar circuitos reativos, isto é,
circuitos que contem resistores, capacitores e indutores. Também, tensões e correntes alternadas
senoidais podem ser representadas por números complexos, facilitando a análise
de circuitos alternados em regime permanente. Mais adiante veremos exemplos de
representação de tensão senoidal.
ELEMENTOS
COMPLEXOS ESPECIAIS
- Igualdade
de números complexos:
Sejam os números complexos z = a + jb e w = c + jd, define-se igualdade entre z e w, se forem satisfeitas as
seguintes condições.
Z = w se, e somente se, a = c e
b = d
- Oposto
de um número complexo:
Seja um número complexo z = a +jb o seu oposto é:
- z = oposto
de (a+jb) = - (a + jb) = (-a) + j(-b)
- Conjugado
de um número complexo:
Seja um número complexo z = a +jb o seu conjugado é:
z* =
conjugado de (a+jb) = a + j.(-b)
Um número complexo
pode ser representado em quatro formas:
a)
Forma
retangular:
b)
Forma polar ou
de Steinmetz: o número complexo é representado por seu módulo e ângulo.
c) Forma trigonométrica:
d)
Forma
exponencial ou de Euler:
Plano de
Argand-Gauss (plano dos complexos). Veja gráfico a seguir:
A transformação de
retangular para polar (sem uso de calculadora) tem que levar em consideração o quadrante em que está o
número complexo.
Exemplos:
Transformar de retangular para polar os seguintes
números complexos:
a)
3 + j4
b)
3 – j4
c)
– 3 + j4
d)
– 3 – j4
Para facilitar, escolhemos o Terno Pitagórico
(3,4,5).
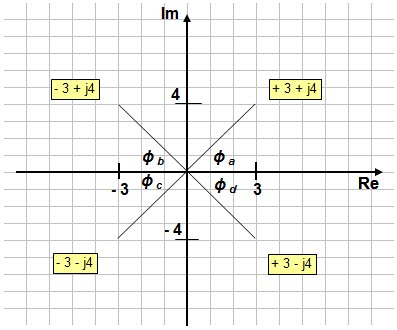
Vamos desenhar a localização no plano dos complexos:
No caso (a):
(+3 + j4) nitidamente encontra-se no 1º quadrante
do plano dos complexos.
No caso (b):
(+3 – 4j) é fácil ver que está no 4º quadrante do
plano dos complexos.
No caso (c): (recomenda-se uma atenção redobrada neste ponto, pois podemos ser traídos pela
calculadora)
Pelos cálculos podemos observar (erroneamente) que
está no 4º quadrante (como no caso (b)), mas na realidade, está no 2º
quadrante (podemos observar no desenho feito no início). Portanto,
justifica-se aqui a importância do desenho feito inicialmente, pois sem este
desenho no plano complexo, podemos cometer erro facilmente.
De fato, o número complexo do item (c) está no 2º
quadrante. Para ver isso, fazemos uma pequena manipulação algébrica:
De forma mais direta, temos que, conforme a figura
inicial, que o ângulo é simplesmente:
Φ = 180º - 53,13º = 126,87º
No caso (d): (requer a mesma atenção do item anterior)
Observando apenas os resultados da calculadora,
podemos chegar a uma conclusão errada (de que a localização é no 1º quadrante),
porém, examinando-se diretamente o número complexo em questão, nota-se que
tanto a parte real como a imaginária, são negativas, o que leva-nos à conclusão
que de fato este número complexo está no 3º quadrante.
OPERAÇÕES COM NÚMEROS COMPLEXOS
Soma e
Subtração
Para somar e subtrair dos números complexos,
soma-se ou subtrai-se suas correspondentes partes reais e imaginárias.
Sejam A = (a+jb) e B = (c+jd)
Então: A ± B = (a+jb) ± (c+jd) = (a ± c) + j(b ± d)
Produto
Sejam A = (a+jb) e B = (c+jd)
O produto de A e B é dado por:
A*B =
(a+jb)*(c+jd) = (ac – bd) + j(ad + bc)
Lembram as operações com expressões polinomiais:
Produto na forma polar:
Divisão
Para a divisão entre complexos, deveremos, primeiro
aprender a inverter um número complexo.
Seja um número complexo z = a +bj, não nulo (a ou b deve ser
diferente de zero), então, podemos definir o inverso de z como:
Tal que
O produto de z
pelo seu inverso z-1 deve
ser igual a 1, isto é:
(a+bj).(u+jv) =
(au-bv)+j(av+bu) = 1 = 1 + j0
O que nos leva a um sistema com duas equações e
duas incógnitas:
au – bv =1
bu + av = 0
Resolvendo o sistema, temos:
Assim, o inverso do número complexo (z = a
+ jb) é:
Exemplo:
Obter o inverso de seguinte número complexo: z = 5
+ j12
O inverso de um
número complexo pode ser obtido, também, pela multiplicação do numerador e
denominador pelo conjugado de z:
Então, a
divisão entre números complexos é:
Sejam z = a +jb e w = c +jd (w diferente de
zero), a divisão de z por w é definida como o número complexo obtido pelo
produto entre z e w-1, isto é,
Exemplo:
Dividir o número z = 2 + j3 por w = 5 + j12.
Basta multiplicar o numerador (z) por inverso do
divisor (w-1).
O inverso de w é:
Portanto,
Outra maneira de
executar a divisão:
Para dividir o número complexo z = 2 + j3 por w = 5
+ j12, basta multiplicar o numerador e o denominador da fração z/w pelo
conjugado de w:
Divisão na forma polar:
NÚMEROS COMPLEXOS
APLICADO À ELETRICIDADE EM CORRENTE ALTERNADA (CA)
Um número complexo tem módulo e fase. Isso
possibilita em representar um sinal senoidal, também, por um número complexo,
sendo a amplitude e a fase inicial do sinal correspondentes, respectivamente,
ao módulo e o ângulo do número complexo.
Terminologia (=nomenclatura) utilizadas
matematicamente:
Expressão trigonométrica:
Onde:
v(t)
≡
tensão instantânea (variável) → letra minúscula;
Vp
≡
tensão de pico (valor fixo) → letra maiúscula;
Expressão em número complexo:
Onde:
v(t)
≡
tensão instantânea (variável) → letra minúscula;
Vp
≡
tensão de pico (valor fixo) → letra maiúscula;
Exemplo:
Representar as tensões v1(t) e v2(t)
a seguir na forma de números complexos (na forma polar):
NOTA:
No caso de tensões, correntes e
potências elétricas representadas por números complexos, os módulos podem ser
dados tanto por valores de pico quanto por valores eficazes.
Representação de Corrente Alternada (CA)
Expressão trigonométrica:
Número complexo:
Justificação: