Resoluções no final desta lista
1) (FUVEST) Sendo i a unidade imaginária (i2 =
-1) pergunta-se: quantos números reais a existem para os quais (a + i)4 é
um número real?
a)
1
b)
2
c)
3
d)
4
e)
infinito
2) (FUVEST) Sabendo que k é um número real e que a
parte imaginária do número complexo z=(2+i).(k+2i)-1 é zero, então k
é igual a:
a)
– 4
b)
– 2
c)
1
d)
2
e)
4
3) (FUVEST) Dado o número complexo z = √3 + i, qual o menor valor do
número inteiro n > 0 para o qual zn é um número real?
a)
2
b)
4
c)
6
d)
8
e)
10
4) Converta de forma retangular para polar.
z
= 20 – j10
5) Converter de forma retangular para polar:
z
= 10 + j15
6) (FEI-67) Escrever o número complexo
na forma (a + bi) e na forma trigonométrica.
7) (MACK-70) Escreva na forma trigonométrica o
inverso multiplicativo de (1+i√3).
8) Colocar na forma polar o seguinte número
complexo:
9) Dados os números complexos
z1
= ρ1*(cosθ1 + i*senθ1)
z2
= ρ2*(cosθ2 + i*senθ2)
determinar
│z1 + z2│ e mostrar que │z1 + z2│≤
│z1│+│z2│
10) Transformar
na forma polar o número complexo:
Soluções
1)
Desenvolvendo o binômio, temos:
(a+1)4 = (a+1)2.(a+1)2=
(a²+2ai+i²).(a²+2ai+i²)= a4+4a³i-6a²+1 =
(a4 - 6a² + 1) + (4a³ - 4a)i
Para
que tenhamos um número real, a parte imaginária tem de ser zero.
Logo,
(4a³ - 4a) = 0 ↔ 4a(a² - 1) =0 ↔
4a = 0, ou a² - 1 = 0
Portanto,
a = 0, ou a = 1, ou a = -1
Resposta: Existem 3 valores de a
que torna (a+i)4 um número real e, portanto,
a alternativa correta é a letra C.
2)
Multiplicando o numerador e o denominador pelo
conjugado do número complexo (k+2i); e sabemos que i² = - 1; temos:
Para que a parte imaginária seja
zero: (k-4) = 0, portanto, k = 4
Resposta: A alternativa correta
é E.
3)
O segredo deste tipo de
problema é trabalhar com número complexo na forma trigonométrica (forma polar)
Portanto, o número complexo na
forma polar (trigonométrica) é:
z
= 2.(cos30º + i.sen30º)
Aplicando
a fórmula de Moivre, temos:
zn
= 2n(cos(30º.n) + isen(30º.n))
Para
que zn seja um número real, devemos ter a sua parte imaginária nula,
isto é: sen(30º.n) = 0
Por
outro lado, para que o seno de um ângulo seja zero, devemos ter um ângulo na forma k.180º, onde k é um
número inteiro.
Logo, n.30º = k.180º → n.30º = k.6.30º → n = 6k
Como
k é um número inteiro (k = ..., -1, 0, 1, 2, 3, ...), portanto,
n
= ..., -12, -6, 0, 6, 12, 18, ...
O
enunciado pede o menor valor positivo de n, portanto, concluímos que n = 6.
Resposta: A alternativa correta é
a letra C.
4)
O segredo para não errar a localização do ângulo
é sempre bom colocar o número complexo no plano imaginário x real.
Observamos que está no IV quadrante.
5)
Fazendo o gráfico de Argand-Gauss:
Está no I quadrante.
Portanto,
6) Multiplicando pelos respectivos conjugados para
eliminar os i’s no denominador:
Portanto, na forma z = a + bi é:
Agora vamos escrever na forma trigonométrica:
(No plano
de Argand-Gauss)
A forma trigonométrica é: z = │z│. (cosϕ + i.senϕ), portanto,
7) Sabemos que em matemática o inverso
multiplicativo de um número x é o número y que multiplicado por x, gera a
identidade.
Então,
No plano de Argand-Gauss:
Logo, na forma trigonométrica é:
8) Representando no plano Argand-Gauss, temos:
9)
10)
Colocando no plano Argand-Gauss
Portanto:




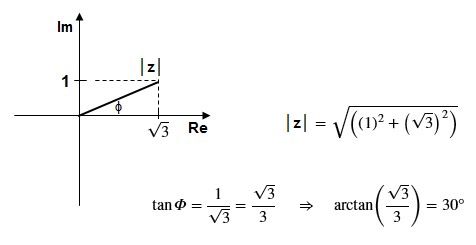


















Nenhum comentário:
Postar um comentário