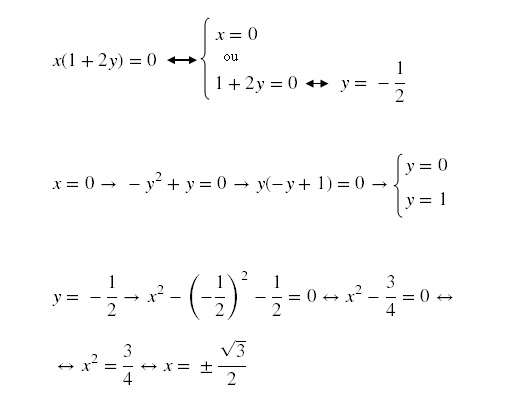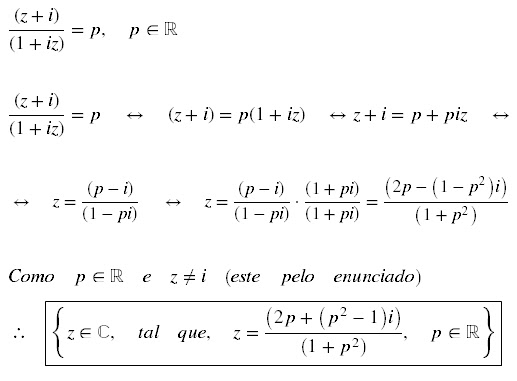FUVEST-Polinômios-Ex.Resolvidos

Veja no Matemática-2015.  clique aqui

Dispositivo de Briot-Ruffini

Sejam P(x) e Q(x) polinômios da seguinte forma:

A raiz de Q(x) é:

Os coeficientes de P(x) são:

Montagem do dispositivo de Briot-Ruffini:

Descrição do procedimento:

1) Colocar a raiz de Q(x) à esquerda e os coeficientes de P(x) à direita;

2) Reescrever o primeiro coeficiente na linha de baixo;

3) Multiplica-se o primeiro coeficiente por α (raiz de Q(x)) e somado com o segundo coeficiente.  O resultado é colocado abaixo do segundo coeficiente;

4) O resultado do item anterior é multiplicado por α e somado com o terceiro coeficiente e o resultado é colocado abaixo do terceiro coeficiente;

5) Assim por diante, até se acabarem os coeficientes;

6) O último valor encontrado é o resto da divisão;

7) Os demais resultados encontrados na linha inferior são os coeficientes do polinômio desejado.

Exemplo:

A raiz de Q(x) é:

Portanto, o polinômio P(x) fica:

Polinômio

Definição

Dada a sequência de números complexos  (a₀, a₁, a₂, ..., a_n), consideremos a função: f: C→ C  dada por f(x) = a₀ + a₁x + a₂x² + ... + a_nxⁿ.  A função f é denominada função polinomial ou polinômio associado à sequência dada.

O números a₀, a₁, a₂, ..., a_n  são chamados coeficientes e as parcelas = a₀, a₁x, a₂x², ..., a_nxⁿ  são chamados termos do polinômio f.

Exemplos:

Definição

Dados o número complexo a e o polinômio f(x) = a₀ + a₁x + a₂x² + ... + a_nxⁿ, chama-se valor numérico de f em a a imagem de a pela função f, isto é:

Assim, por exemplo, se f(x) = 2 + x + x² + 3x³, temos:

Em particular, se a é um número complexo e f  (f = f(x)) é um polinômio tal que f(a) = 0, dizemos que a é uma raiz ou um zero de f.

Por exemplo, os números ‒ 2 e ‒ 1 são raízes de f(x) = 2x + 3x² + x³, pois:

f(‒2) = 2(‒2) + 3(‒2)² + (‒2)³ = 0

f(‒1) = 2(‒1) + 3(‒1)² + (‒1)³ = 0

POLINÔMIO NULO

Definição

Um polinômio f é nulo (ou identicamente nulo) quando f assume o valor numérico zero para todo x complexo.  Em símbolos, tem-se:

Teorema

Um polinômio f é nulo se, e somente se, todos os coeficientes de f forem nulos.  Em símbolos, sendo f(x) = a₀ + a₁x + a₂x² + ... + a_nxⁿ, tem-se:

IGUALDADE DE POLINÔMIOS

Definição

Dois polinômios f e g são iguais (ou idênticos) quando assumem valores numéricos iguais para todo x complexo.  Em símbolos, tem-se:

Teorema

Dois polinômios f e g são iguais se, somente se, os coeficientes de f e g forem, ordenadamente iguais. Em símbolos, tem-se:

FUVEST - Números Complexos - Ex.Resolvidos

EX-01 (FUVEST 2000)

a) Determine todas as soluções, no campo complexo, da equação , onde i é a unidade imaginária, isto é,  é o conjugado de z.  

b) Represente essas soluções no plano complexo, usando o sistema de coordenadas desenhado ao lado.

Solução:

a)

Seja z = x + yi um número complexo, com x,y ϵ R.

Para que a expressão (1) seja zero devemos ter as seguintes condições:

Logo, temos:

Portanto, temos:

Resposta:  

b)

EX-02 (FUVEST 2001)

No plano complexo, cada ponto representa um número complexo.  Nesse plano, considere o hexágono regular, com centro na origem, tendo i, a unidade imaginária, como um de seus vértices.

a) Determine os vértices do hexágono.

b) Determine os coeficientes de um polinômio de grau 6, cujas raízes sejam os vértices do hexágono.

Solução:

a)

Da simetria da figura, temos que:

b)

Os números complexos z que são os vértices do hexágono podem ser descritos como:

Como cos(π+2kπ) = ‒1 e sen(π+2kπ) = 0, então,

Logo, o polinômio é da forma P(x) = x⁶ +1

Portanto, P(x) = ax⁶ + bx⁵ + cx⁴ + dx³ + ex² + fx + g

Então, por comparação, temos:

a = g = 1    e    b = c = d = e = f = 0

EX-03 (FUVEST 2003)

Nos itens abaixo, z denota um número complexo e i a unidade imaginária (i² = -1). Suponha z ≠ i.

a) Para que valores de z tem-se  

b) Determine o conjunto de todos os valores de z para os quais  é um número real.

Solução:

a)

b)

EX-04 (FUVEST 2004)

Considere a equação  , onde α é um número real e indica o conjugado do complexo z. 

a) Determine os valores de α para os quais a equação tem quatro raízes distintas.

b) Representar,  o plano complexo, as raízes dessa equação, quando α = 0.

Solução

a)

Seja z = x + yi um número complexo com x e y números reais (x, y ϵ R), então:

Para que tenhamos essa igualdade (Eq-1), devemos ter (por comparação):

Portanto, a equação  admitir quatro raízes distintas se, e somente se, a equação  admitir duas raízes reais e distintas e  , ou seja, 

b) Para α = 0

Logo, como z = x + yi, temos:

EX-05 (FUVEST 2006)

Determine os números complexos z que satisfazem, simultaneamente,  

Lembretes: i² = -1, se w = a +bi, como a e b reais, então 

Solução:

Seja  z = a +bi com a, b ϵ R, então:

( 2 ): b = a + 2,  em ( 1 )

EX-06 (FUVEST 2008)

A figura na página de respostas representa o número no plano complexo, sendo  a unidade imaginária. Nessas condições, 

a) determine as partes real e imaginária de 1/w e de w³.

b) represente 1/w e de w³ na figura ao lado.

c) determine as raízes complexos da equação z³ - 1 = 0.

Solução:

a)

Aplicando a forma polar:

Calculando o argumento e módulo de 

(1) Se θ = argumento, então temos que: 

(2) 

Portanto, a forma polar de

Logo:

Portanto, as partes real e imaginário de 1/w e de w³ são:

b)

As formas polares são:

Representando 1/w e de w³ na figura, temos:

 c)

EX-07 (FUVEST 2011)

a) Sendo i a unidade imaginária, determine as partes real e imaginária do número complexo. 

b) Determine um polinômio de grau 2, com coeficientes inteiros, que tenha z₀ como raiz.

c) Determine os números complexos w tais que z₀.w tenha módulo igual a 5√2 e tais que as partes real e imaginária de z₀.w sejam iguais.

d) No plano complexo, determine o número complexo z₁ que é o simétrico de z₀ com relação à reta de equação y – x = 0.

Solução:

 a)

b)

Se z₀ é raiz, o seu conjugado também é raiz.

c)

Portanto, por comparação, temos:

Do enunciado: partes real e imaginária de z₀.w são iguais, então:

(2) em (1), 

d) 

EX-08 (FUVEST 2015)

Resolva os três itens abaixo:

(a) Calcule .

(b) Dado o número complexo  , encontre o menor inteiro n > 0 para o qual zⁿ seja real. 

(c) encontre um polinômio de coeficientes inteiros que possua z como raiz e que não possua raiz real.

Solução:

a) Calculando cos(3π/8) e sen(3π/8)

Sabemos que: 

b)

Logo, o menor valor inteiro de n > 0 ocorre para k = 3, assim, 

c)

Portanto, um polinômio com raiz z, sem raízes reais e com coeficientes inteiros é :